The core of any parametric CAD program is its geometric constraint solver. The solver starts with geometric properties of the sketch, like a line length or an angle or a tangency. Based on these properties, it calculates a simple representation of the sketch's lines, points, and curves.

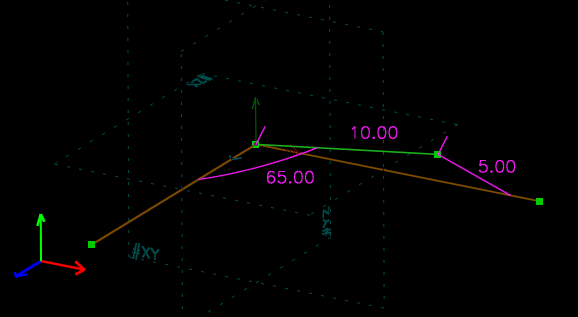
For a trivial example, we might specify that a point lies 10 mm from the origin, and 5 mm from the x-axis. We also specify that the line from the origin to that point makes a 65° angle with the z-axis. That point turns out to have (x, y, z) = (8.66, 2.67, 4.23), after solving three equations in three unknowns. A real sketch may involve hundreds of unknowns.

In SolveSpace, constraints are represented as equations in a symbolic algebra system. In general, these equations are solved numerically, by a modified Newton's method. Some special cases are handled, for any equation that can be solved by forward-substitution, and equations that are solvable alone.

If the sketch is not fully constrained, then the Jacobian is solved in a least squares sense, with each equation written in such a way as to make the quantity being minimized a useful penalty metric. This tends to yield "less surprising" results when dragging points in an underconstrained sketch, compared to approaches that use weak dimensions to keep the sketch always fully constrained.

A failure to converge almost always results from a real problem with the specified constraints. For example, a sketch that describes a linkage will fail to converge when the real linkage would bind. If multiple solutions exist, then the initial position of the sketch determines which is chosen. The natural result (according to the basin of attraction of the numerical method) is generally a reasonable choice, though some cases are handled specially.

In general, constraints apply in 3d. A constraint may also apply projected into a workplane. For example, a constraint on the distance between two points may actually apply to the distance between the projections of those two points into the specified plane. Angle, point-coincident, and point-on-curve constraints are similarly available in projected forms.

The constraint solver used in SolveSpace is available separately as a library.